SOFTWARE TÉCNICO GRATUITO

Software de ingeniería

En www.topoedu.es siempre hemos apostado por el software de CALIDAD TÉCNICA. Por ello, desde hace una década venimos desarrollando programas informáticos, innovadores, que han resultado de gran ayuda a más de 30.000 usuarios.

Para establecer una coherencia en todos programas gratuitos que ofrecemos, vamos a actualizad todos los programas de esta sección. Poco a poco iremos colgando las nuevas versiones, cuya ruta de instalación será la misma en todos los casos. De esta manera, podrás tener todos tus programas en una misma sección de tu PC. Por ello, de momento, no podrás descargar los programas hasta que sean actualizados a la nueva versión. No obstante, te dejamos las referencias de las antiguas versiones para que puedas hacerte una idea de sus funcionalidades.

Listado de programas gratuitos
Compatibles con

ToDXF v.1.0 [Próxima actualización: ToDXF v.2. Más herramientas. Más potente. Totalmente gratuito]

TEMÁTICA: Topografía y delineación
Fecha lanzamiento: Abril 2012
Autor: Eduardo Renard Julián (topoedu@terra.es)
Tamaño: 31MB

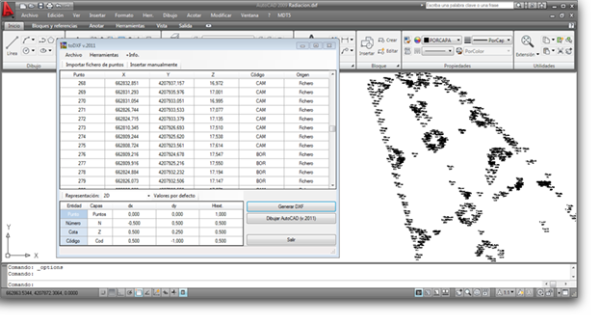
ToDXF es un programa gratuito que te permitirá pasar ficheros de puntos, tipo XYZ, YXZ, NEZ, ENZ, a AutoCAD. Por fin podrás representar en AutoCAD un listado de puntos (sin límite de cantidad), clasificando los elementos de los puntos por capas (Número, Punto, Cota y Código), y de la manera fácil y amena.

Características:

• Importa ficheros de puntos. Formatos soportados GSI. IDX, SYS, DAT, RAW, TXT, y PUN.
  

• Genera un fichero DXF o dibuja directamente sobre AutoCAD la nube de puntos.
  

• Clasifica los atributos de los puntos por capas (Número, Punto, Código y Cota).
  

• Opciones disponibles; modificación de nombres de capa y posición de los puntos.
  

Ole.NET v.2.0 [Próxima actualización: Ole.NET v.2.1]

TEMÁTICA: Ingeniería Marítima y Costera
Fecha lanzamiento: Febrero 2013
Autor: Eduardo Renard Julián (topoedu@terra.es)
Tamaño: 3,8MB

En 1967 Hasselmann añadió un concepto que constituiría la teoría más aceptada en nuestros días. Según Hasselmann, las olas interactuaban entre sí y compartían la energía. Por ello, era posible el transporte de energía dentro del espectro entre algunas frecuencia determinadas, que explicaba el crecimiento al principio de la formación de las olas.

Actualmente se han logrado grandes progresos en el estudio de las olas, facilitándose pronósticos útiles que permiten desde impedir tragedias hasta el aprovechamiento del oleaje como fuente de energía. A ello ha colaborado el diseño de nuevos aparatos de medición y los modelos artificiales a escala de las olas; los nuevos métodos de observación de las olas naturales en las boyas y plataformas flotantes, y el empleo de satélites que permiten recoger datos en unos 40.000 lugares de la atmósfera y del océano cada día.

El programa Ole.NET está especialmente diseñado para trabajar y gestionar datos relacionados con el oleaje.
Ole.NET es un software gratuito para cálculos de obras marítimas.

Potencial de cálculo:

• Definición de parámetros de una ola. Celeridad, frecuencia, peralte, altura relativa, profundidad relativa, sobre elevación, número de onda, frecuencia angular y tipo de profundidad. Ole.NET se basa en los parámetros de inserción; longitud de onda, altura, amplitud, periodo, profundidad, N.M.R. y N.M.M.
  

• Longitud y celeridad en función del calado. Para el tipo de profundidad (aguas someras, aguas profundas, y aguas transicionales), se determinan la longitud y velocidad de fase. Los métodos disponibles son: Método de Fenton McKee, y Método de Eckart.
  

• Rotura de ola: bajo dos supuestos. Criterio I: función de parámetros locales de la ola y características batimétricas, ó Criterio II: función de características batimétricas y peralte de ola.
  

Los métodos de cálculo implementados en el programa, bajo estos dos criterios, son:

Todos los datos calculados por Ole.NET son exportables a formato ASCII.

CEEP v.1.0 [Próxima actualización: CEEP v.2. Completamente profesional. Herramientas de análisis de errores de cierre teóricos y experimentales]

TEMÁTICA: Topografía
Fecha lanzamiento: Septiembre 2006
Autor: Eduardo Renard Julián (topoedu@terra.es)
Tamaño: 1MB

CEEP es un programa gratuito, descargado por más de 15.000 USUARIOS, que te permitirá obtener los errores teóricos que una estación total comete al realizar una determinada poligonal. Además, puedes comparar los errores de cierre teóricos con los experimentales.

Tan sencillo de usar como seguir estos pasos:

• Insertar los parámetros de poligonal (longitud y tramos).
  

• Seleccionar el instrumento de una base de datos con más de 350 modelos, o insertar las características técnicas del instrumento (aumento, desviaciones estándar, etc.).
  

• Comprobar los errores teóricos que el instrumento comete en la poligonal.
  

• Imprimir un informe con un resumen del cálculo.
  

Este programa incluye un manual de usuario con ejemplos de aplicación.

EvapoCalc v.1.0 [Próxima actualización: EvapoCalc v.2.  Ampliamanete mejorado. Compatible con todas las versiones Windows]

TEMÁTICA: Ingeniería Hidrológica
Fecha lanzamiento: Junio 2013
Autor: Eduardo Renard Julián (topoedu@terra.es)

Tamaño: 1MB

El concepto de evaporación es el resultado del proceso físico, por el cual el agua cambia de estado líquido a gaseoso, retornando, directamente, a la atmósfera en forma de vapor. También el agua en estado sólido (nieve, hielo) puede pasar directamente a vapor. Este fenómeno se conoce como sublimación. A efectos de estimar las pérdidas por evaporación en una zona, el término se entenderá en sentido amplio, incluyendo la sublimación. No se incluye en cambio, la evaporación de las gotas de agua en su recorrido descendente antes de alcanzar la superficie de la tierra, pues en ningún momento estas se contabilizan como aportación (precipitación) en un hipotético balance hídrico.

La evaporación es un cambio de estado, y precisa una fuente de energía que proporcione a las moléculas de agua, la suficiente para efectuarlo. Esta energía procede de la radiación solar, tanto de forma directa como indirecta. Disponemos de varios métodos de cálculo y, de todos ellos, EvapoCalc presenta los siguientes:

Método de balance de energía
La evaporación de agua requiere cantidades relativamente altas de energía, ya sea en la forma de calor sensible o de energía radiante. Por ello, el proceso de evapotranspiración es controlado por el intercambio de energía en la superficie de la vegetación y es limitado por la cantidad de energía disponible. Debido a esta limitación, es posible predecir la evapotranspiración aplicando el principio de conservación de energía. La energía que llega a la superficie debe ser igual a la energía que sale de la superficie en el mismo periodo de tiempo.

Método aerodinámico
Además del suministro de energía calórica, el segundo factor que controla la tasa de evaporación desde una superficie abierta de agua es la habilidad para transportar el vapor lejos de la superficie. La tasa de transporte se determina por el gradiente de humedad en el aire cercano a la superficie y la velocidad del viento a través de dicha superficie, y estos dos procesos pueden analizarse utilizando simultáneamente las ecuaciones de transporte de masa y de cantidad de movimiento en el aire.

Método combinado aerodinámico y balance de energía
La evaporación puede calcularse utilizando el método aerodinámico cuando el suministro de energía no es limitante, y aplicando el método de balance de energía cuando el transporte de vapor tampoco es limitante. Pero, normalmente, estos dos factores son limitantes, luego es necesaria una combinación de los dos métodos. En el método del balance de energía es difícil calcular el campo de flujo de calor sensible H. Pero como el calor se transfiere por convección a través del aire que se localiza encima de la superficie del agua, y el vapor de agua se transfiere por convección, en forma similar puede suponerse que el campo de flujo de calor del vapor y el campo de flujo de calor sensible son proporcionales, en donde la constante de proporcionalidad se conoce como la relación de Bowen (Bowen, 1926).

Método Priestley-Taylor
El método de combinación es apropiado para aplicarse a áreas pequeñas con información climatológica detallada. La información requerida incluye la radiación neta, la temperatura del aire, la humedad, la velocidad del viento y la presión del aire. Cuando parte de esta información no está disponible, deben utilizarse las ecuaciones de evaporación más simples que requieren menos variables. En el caso de la evaporación sobre áreas grandes, las consideraciones de balance de energía dominan la tasa de evaporación. Para tales casos Priestley y Taylor (1972) determinaron que el segundo término de la ecuación de combinación es aproximadamente 30% del primero, luego la ecuación de combinación anterior puede reescribirse como la ecuación de evaporación de Priestley‐Taylor.

Todos los cálculos efectuados por EvapoCalc se pueden exportar a ficheros ASCII.